【速報】OpenAIの新モデル「OpenAI o1」とは?ChatGPTでも利用可能!驚きの性能を解説
OpenAIは、難しい問題を解決するための新しいAIモデルシリーズ「OpenAI o1-preview」を発表しました。このモデルは、人間のように回答前に時間をかけて思考するよう設計されており、科学、コーディング、数学などの複雑なタスクでこれまでのモデルよりも優れた性能を発揮するとされてます。
本記事では、OpenAIの発表内容の解説に加えて、実際に算数の問題を解かせたうえで、性能の確認をしてみようと思います。
OpenAI o1の特徴
OpenAI o1シリーズは、人間のように回答前に時間をかけて深く思考するよう設計されたAIモデルです。主な特徴は以下の通りです。
- 高度な推論能力: 科学、コーディング、数学などの複雑なタスクで、これまでのモデルを超える性能を発揮します。
- 自己改善: トレーニングを通じて、思考プロセスを洗練し、多様な戦略を試行し、誤りを認識して修正する能力を持ちます。
- 安全性の向上: 新しい安全トレーニング手法により、ユーザーが安全ガイドラインを回避しようとする試みに対して高い耐性があります。
これらの特徴により、OpenAI o1は従来のモデルでは困難だった高度な問題解決を可能にします。
OpenAI o1-previewとo1-miniの違い
OpenAIは、異なるニーズに応えるために2つのモデルを提供しています。
o1-preview
- 概要: フルスペックのモデルで、高度な推論能力を持ちます。
- 適用範囲: 科学研究、複雑な数学の問題、難解なコーディングタスクなど。
- 特徴:
- 物理学、化学、生物学の難関ベンチマークで博士課程の学生と同等の性能。
- 国際数学オリンピック(IMO)の予選試験で83%の正答率。
o1-mini
- 概要: コーディングに特化した高速・低コストのモデル。
- 適用範囲: 日常的なコーディングタスク、コストを抑えたい開発環境。
- 特徴:
- o1-previewより80%安価。
- 高速な応答時間で効率的にコーディング問題を解決。
OpenAI o1をChatGPTで利用する方法
ChatGPT PlusおよびTeamのユーザーは、以下の手順でo1モデルにアクセスできます。
- モデルの選択: ChatGPTのモデル選択メニューから「o1-preview」または「o1-mini」を選択します。
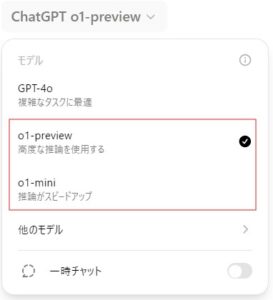
- 利用制限の確認:
- o1-preview: 週30メッセージまで利用可能。
- o1-mini: 週50メッセージまで利用可能。
- 今後の予定:
- レート制限の緩和や、ChatGPTが自動的に最適なモデルを選択する機能の追加が予定されています。
- ChatGPT EnterpriseとEduのユーザーは、来週から両モデルにアクセス可能になります。
- o1-miniは、将来的にChatGPT無料ユーザーにも提供予定です。
OpenAI o1-previewに数学の問題を解かせてみた
整数に関する問題
【問題(プロンプト)】
n^3 − 7n + 9が素数となるような整数nを全て求めよ。
数学的な論証とともに、日本語で回答をしてください。
【ChatGPT o1-previewの回答】
が素数となるような整数 を求めるために、まずいくつかの整数値を代入して調べてみます。
のとき:
これは素数です。
のとき:
15 は素数ではありません。
のとき:
これも素数ではありません。
のとき:
9 は素数ではありません。
のとき:
3 は素数です。
のとき:
これも素数です。
のとき:
素数ではありません。
のとき:
素数ではありません。
のとき:
が 4 以上の整数の場合、の項が急激に増加するため、結果として得られる数は非常に大きくなり、素数である可能性は低くなります。同様に、 の場合も大きな負の数となり、素数にはなりません。
以上の調査より、 が素数となるのは以下の場合のみです。
- のとき、値は 3(素数)
- のとき、値は 3(素数)
- のとき、値は 3(素数)
結論:
が素数となる整数 は、 である。
答え
答えはあっておりますが、数学的な論証は未だ弱いです(上記オレンジ部分)
ちなみに、更問下記の更問をしたところ、正答を引き出すことができました(多分)
【追加プロンプト】
以下の部分を数学的に正しく論証してください
n が 4 以上の整数の場合、急激に増加するため、結果として得られる数は非常に大きくなり、素数である可能性は低くなります。同様に、
n≤−4 の場合も大きな負の数となり、素数にはなりません。
【ChatGPT o1-previewの回答】
証明:
が素数となる整数 を求めるために、の範囲ごとに数学的に検証します。
1. 任意の整数 に対して、は 3 の倍数であることの証明
まず、を 3 で割った余りに基づいて場合分けします。
-
(i) の場合:
と置くと、
これは明らかに 3 の倍数です。
-
(ii) の場合:
と置くと、
展開すると、
各項を 3 で割ると、余りは 0 になります。
-
(iii) の場合:
と置くと、
展開すると、
これも 3 の倍数となります。
したがって、任意の整数 に対して、は 3 の倍数です。
2. が素数となる場合の特定
とすると、
この三次方程式の整数解を求めます。
因数分解すると、
さらに二次式を因数分解すると、
したがって、解は です。
3. および の場合の検証
-
の場合:
では、の項が急激に増加します。を代入すると、
45 は 3 の倍数であり、3 より大きいので合成数です。一般に、のとき、となり、常に合成数となります。
-
の場合:
を代入すると、
結果は負の数であり、素数ではありません。一般に、 のとき、となり、素数にはなりえません。
結論
- のときのみ、となり、3 は素数です。
- 他の整数 では、は 3 の倍数であり、3 より大きい場合は合成数、負の値の場合は素数ではありません。
したがって、数学的に正しく論証しました。
ちょっと怪しい部分はありますが、(おそらく)ほぼ満点の回答が出たと思います。最初のプロンプトを正しく設定することで、おそらく大学入試レベルの問題でも正答できるかと思います。
図形に関する問題
これはちょっと難易度が高そうでしたが、以下の問題を解いてもらいました。
【問題(プロンプト)】
一辺の長さが1の正八面体の互いに平行な2つの面をとり,それぞれの面の重心をG1, G2とする。 G1, G2を通る直線を軸としてこの八面体(内部を含む)を1回転させてできる立体の体積を求めよ。
【ChatGPT o1-previewの回答】

正解は(5/54)*(√6)*πなので、残念ながら不正解でした。。
まとめ
新たなモデルは推論能力が向上している印象は若干ありました。ChatGPT上でも推論の過程(問題文を解析しています、計算しています、といった表示)があり、斬新でした。一方で、より複雑な数学の問題への回答は未だ100%ではないとは思います(実際OpenAIも自社のリリースで、数学オリンピックの予選正答率は83%と発表しております)。また、ChatGPTで利用する際の回答速度が遅い点も気になりました。
普段利用であれば、通常のChatGPTでも性能としては十分ですが、より複雑な推論やコーディングが必要な場合は、ぜひ利用してみてください!
